Survival Analysis

Project Details

Data Description

Lung cancer is a type of cancer that begins in the lungs. Your lungs are two spongy organs in your chest that take in oxygen when you inhale and release carbon dioxide when you exhale. Lung cancer is the leading cause of cancer deaths worldwide and most often occurs in people who smoke. The dataset has multiple variables below. The data comes from R programming language.

inst: Institution code

time (d1): Survival time in days

status (d2): censoring status 1 = censored, 2 = dead

age (i1): Age in years

sex (i2): Male = 1 Female = 2

ph.ecog (i3): ECOG performance score as rated by the physician. 0 = asymptomatic, 1 = symptomatic but completely ambulatory, 2 = in bed <50% of the day, 3 = in bed > 50% of the day but not bed bound, 4 = bed bound

ph.karno (i4): Karnofsky performance score (bad = 0; good = 100) rated by physician

pat.karno (i4): Karnofsky performance score as rated by patient

meal.cal (i5): Calories consumed at meals

wt.loss (i6): Weight loss in last six months

The goal of the data is to understand the survival of lung cancer patients using time-to-event analysis.

What is survival analysis?

It is a collection of statistics for analyzing the expected duration of time until one or more events occur. It is also known as duration analysis, time-to-event analysis, reliability analysis and event history analysis. It can be used in follow fields of research:

1. Medical: Understanding patient survival when diagnosed with a deadly disease.
2. Medical: Hospital readmission duration after a major surgery.
3. Industry: When would battery permanently die/fail.
4. E-commerce: after seeing ads when a person would buy the product.
5. Human resource: When an employee would leave a company.

There are multiple methods used to understand the time to even data. I am going to talk about the following types of models and try to understand their mechanism in time-to-event analysis.

• Kaplan-Meier Estimate (non-parametric)
• COX Proportional Hazard Model (Semi- parametric)
• Accelerated Failure Time Model (Parametric)

Python Packages:

1. Lifelines
2. Matplotlib
3. Pandas
4. numpy

Roadmap:

1. Load the data
2. Analyze and visualize the dataset
3. Imputing missing values
4. Kaplan Meier curve estimation
5. Fitting Cox Proportional Hazard Regression
6. Cox model results interpretation
7. Testing Proportional Hazard assumption
8. Fitting Accelerated Failure Time (AFT) Model
9. AFT model results interpretation

Step 1:

Import packages:

#import libaries
import numpy as np
import pandas as pd
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
from lifelines.utils import median_survival_times
from lifelines import CoxPHFitter
from lifelines.statistics import proportional_hazard_test
from lifelines import WeibullFitter,ExponentialFitter,LogNormalFitter,LogLogisticFitter
from lifelines import WeibullAFTFitter
		    

First, I imported necessary packages for this project.

Numpy will be used for array manipulation.

Pandas will be used for data Manipulation.

Lifelines will be used for survival analysis.

Matplotlib will be used for data visualization.

file_path=r'C:\Users\shang\Desktop\ML\data\lung cancer.csv'
columns=['inst','time', 'status', 'age', 'sex', 'ph.ecog', 'ph.karno','pat.karno', 'meal.cal', 'wt.loss']
df = pd.read_csv(file_path, names=columns)
print(df.head())
		    

I defined the path of where the data file is and set column name as per the lung cancer data information.

Look at the first five-row data in the dataset.

It is very clear that there are some missing values.

Step2: Analyze and visualize the dataset

df=df.drop('inst', axis=1)
df["status"] = df["status"] - 1
df["sex"] = df["sex"] - 1
		    

The status and sex are categorical data. The status consists of 1: censored and 2: dead; while, sex consist of 1: Male and 2 :Female.

As inst variable does not have meaningful information, I drop it. Also, usually categorical data starts from 0, so status and sex variable min 1 to start from 0.

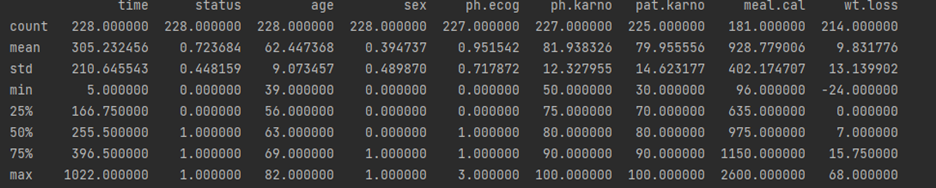
# display base statistical analysis regarding the data
print(df.describe())
		    

From this data description, I can see all the data descriptions on the data, like mean in different measurements, min and max values and 25%, 50% and 75% distribution values.

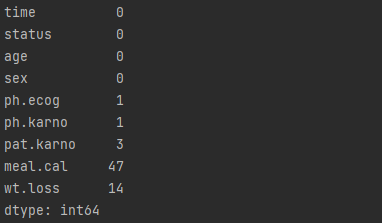
# display summary of missing values
print(df.isnull().sum())
		    

This indicates how many missing values are in each variable.

df["ph.karno"].fillna(df["ph.karno"].mean(), inplace = True)
df["pat.karno"].fillna(df["pat.karno"].mean(), inplace = True)
df["meal.cal"].fillna(df["meal.cal"].mean(), inplace = True)
df["wt.loss"].fillna(df["wt.loss"].mean(), inplace = True)
df.dropna(inplace=True)
df["ph.ecog"] = df["ph.ecog"].astype("int64")
		    

There are several options to address missing values.

1. Remove it entirely but it will reduce the sample when you have a small sample size.
2. Fill in with mean/median or with a particular value.
3. Use k nearest neighborhood model to estimate value.

For this project, I will use option 2 to imputed them with mean of the columns as it is for demonstration purpose. Then, I will remove the NA value of ph.ecog use .dropna() method and converted it to int64.

print(df.isnull().sum())
		    

Run the summary again, I can see all missing values addressed.

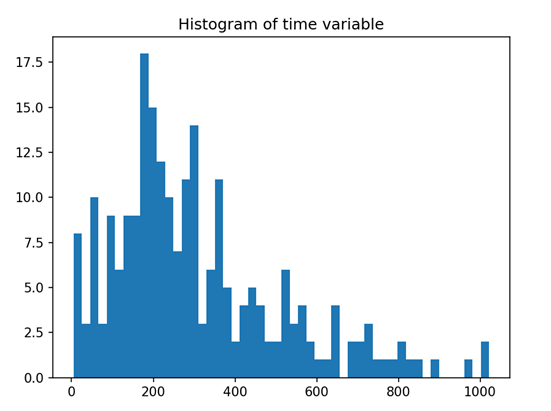
# Data Distribution
T = df["time"]
E = df["status"]
plt.hist(T, bins = 50)
plt.show()
		    

Save time and event/status variable separately in T and E. Plot a histogram of the time variable to see overall idea of the distribution. It indicates the time variable almost follow a log-normal distribution.

Kaplan-Maier Curve Estimation (Non-Parametric)

What is KM?

The Kaplan-Meier approach, also called the product-limit approach, is a popular approach which re-estimates the survival probability each time an event occurs. It is a non-parametric method, means it does not assume the distribution of the outcome variable (i.e., time).

# Kaplan-Meier Curve Estimation
kmf = KaplanMeierFitter()
kmf.fit(durations = T, event_observed = E)
kmf.plot_survival_function()
plt.show()
		    

Initialize kaplan meier object.

Feed duration data and event data.

Plot survival curve.

The plot depicts how the survival probabilities change over time. As the time elapses, the survival probabilities of lung cancer patients reduce.

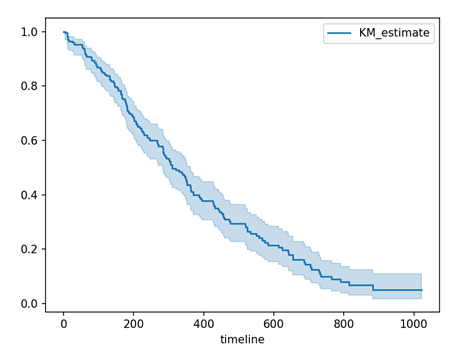
# without 95% confidence interval
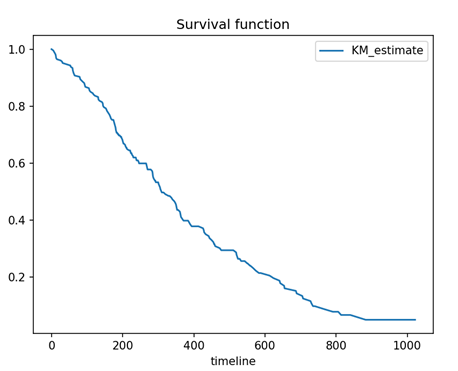
kmf.survival_function_.plot()
plt.title('Survival function')
plt.show()
		    

Plot a survival graph without 95% confidence interval.

#Median Survival Time and Confidence Intervals
median_ = kmf.median_survival_time_
median_confidence_interval_ = median_survival_times(kmf.confidence_interval_)
print("Median survival time:"+str(median_))
print("Median 95% confidence interval:"+str(median_confidence_interval_))
		    

The attribute of KM object can tell me estimation of median survival time and 95% confidence intervals.

It indicates 50% of the sample live 310 days and 50% dies within this timeframe. The 90% CI lower limit is 284 days while the upper is 361 days.

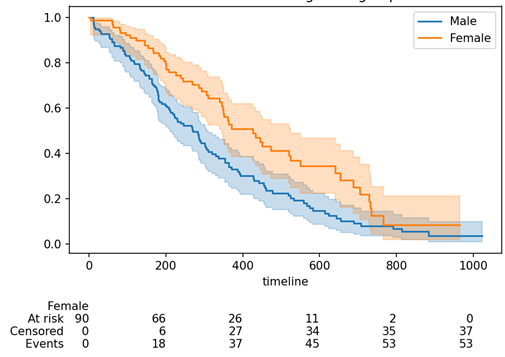
#Gender Categories
ax = plt.subplot()
m = (df["sex"] == 0)
kmf.fit(durations = T[m], event_observed = E[m], label = "Male")
kmf.plot_survival_function(ax = ax)
kmf.fit(T[~m], event_observed = E[~m], label = "Female")
kmf.plot_survival_function(ax = ax, at_risk_counts = True)
plt.title("Survival of different gender groups")
plt.show()
		    

I also want to look at survival probabilities at different gender groups.

Create an axis object.

Create a mask “m” where males are true.

Fit and plot curves for male and female observations.

The curve depicts that female patients are overall higher compared to male patients at any time.

# Anaylze for ph.ecog categories
ecog_types = df.sort_values(by = ['ph.ecog'])["ph.ecog"].unique()
for i, ecog_types in enumerate(ecog_types):
  ax = plt.subplot(2, 2, i + 1)
  ix = df['ph.ecog'] == ecog_types
  kmf.fit(T[ix], E[ix], label = ecog_types)
  kmf.plot_survival_function(ax = ax, legend = False)
  plt.title(ecog_types)
  plt.xlim(0, 1200)
plt.tight_layout()
plt.show()
		    

I plot separate survival curves for other categorical variables. I plot their survival function over a single plot.

Looks like the fourth plot where the ecog==3 is incomplete.

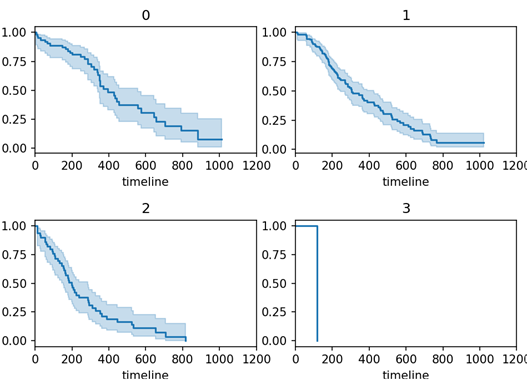
df = df[df["ph.ecog"] != 3]
print(df.shape)
		    

After looking at the data, I notice there is only one record. I just removed it.

In summary, Kaplan-Meier Curve Estimation is useful for estimating the survival probability each time an event occurs for individual or group.

Cox Proportional Hazard Model (Semi-Parametric)

What is Cox-PH model?

Cox-PH model is a semi-parametric model which solves the problem of incorporating covariates. In Cox’s proportional hazard model, the log-hazard is a linear function of the covariates and a population-level baseline hazard.

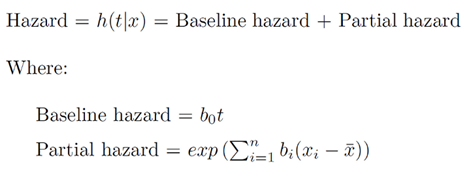
The first term is the baseline hazard and the second term known as partial hazard. The partial hazard inflates or deflates the baseline hazard based on covariates.

Cox proportional hazards regression model assumptions includes:

1. Independence of survival times between distinct individuals in the sample.
2. A multiplicative relationship between the predictors and the hazard.
3. A constant hazard ratio over time.

Definition of Hazard and Hazard Ratio

1. Hazard is defined as the slope of the survival curve. It is a measure of how rapidly subjects are dying.
2. The hazard ratio compares the two groups. If the hazard ratio is 2.0, then the rate of deaths in one group is twice the rate in the other group.

# hot code categorical variable
d_ecog = pd.get_dummies(df["ph.ecog"], prefix = 'ecog')
print(d_ecog.head())
		    

I dummy code the ph.ecog variable and add the prefix for new columns. Here, I will consider ecog_0 as the reference and remove it later.

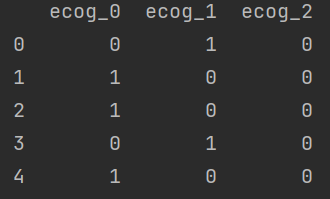
d_ecog = d_ecog[["ecog_1", "ecog_2"]]
df = pd.concat([df, d_ecog], axis = 1)
df = df.drop("ph.ecog", axis = 1)
print(df.head())
		    

Remove ecog_0.

Concatenate the rest of dummy coded variable to main data matrix.

Drop the ecog variable.

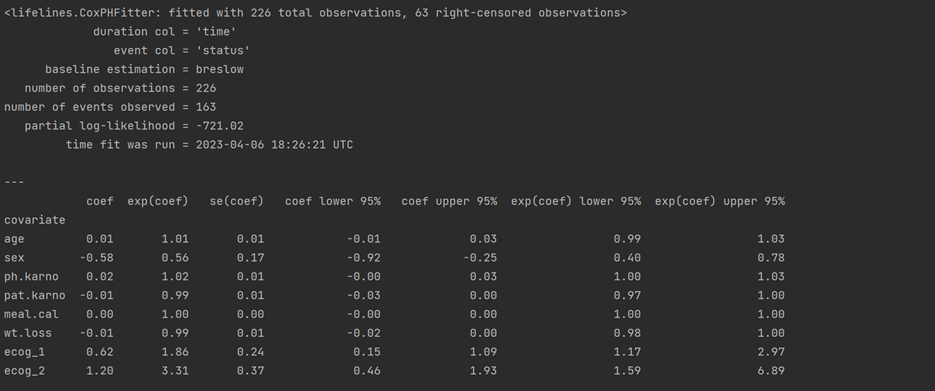
cph = CoxPHFitter()
cph.fit(df, duration_col = 'time', event_col = 'status')
print(cph.print_summary())
		    

Initialize Cox PH object.

Feed time and event data into model.

Display summary.

Sex has a coefficient of about -0.58. I can recall that in the Cox proportional hazard model, a higher hazard means more at risk of the event occurring. So, the value of exp(-0.58) is called the hazard ratio.

It displays that one unit increase in sex containing [0: Male (base) and 1: Female] like from male to female means that baseline hazard will increase by a factor of exp(-0.58)=0.56 approx. 0.6 % decrease.

Similarly, in the ph.ecog variable, the values are: 0= asymptomatic, 1= symptomatic but completely ambulatory and 2 = in bed less than 50% of the day. The coefficient with ecog_1, exp(0.62), is the value of ratio of hazards with being “symptomatic” compared to asymptomatic. This indicates the risk of event is 1.86 times for patients who are symptomatic compared to asymptomatic patients.

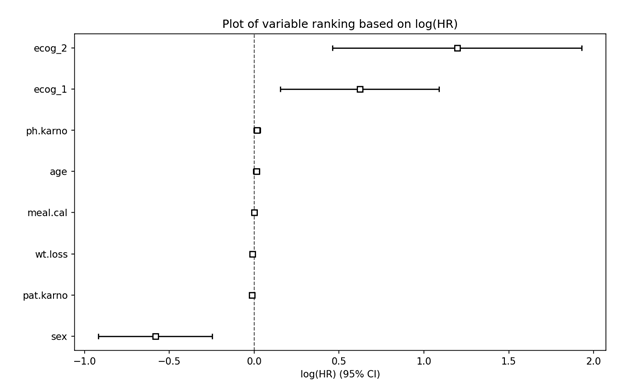
#Plot of variable ranking based on log(HR)
plt.subplots(figsize = (10, 6))
cph.plot()
plt.title("Plot of variable ranking based on log(HR)")
plt.show()
		    

It is clear that sex, ecog_1 and ecog_2 are important than other variables.

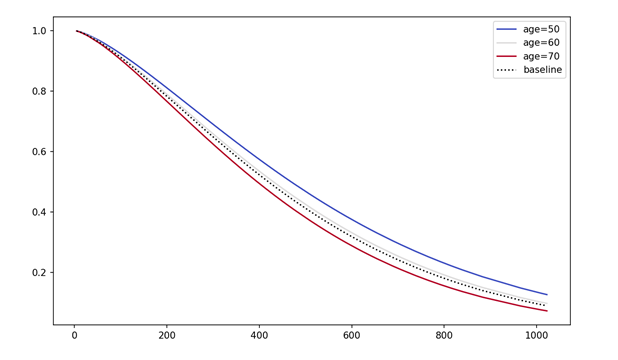
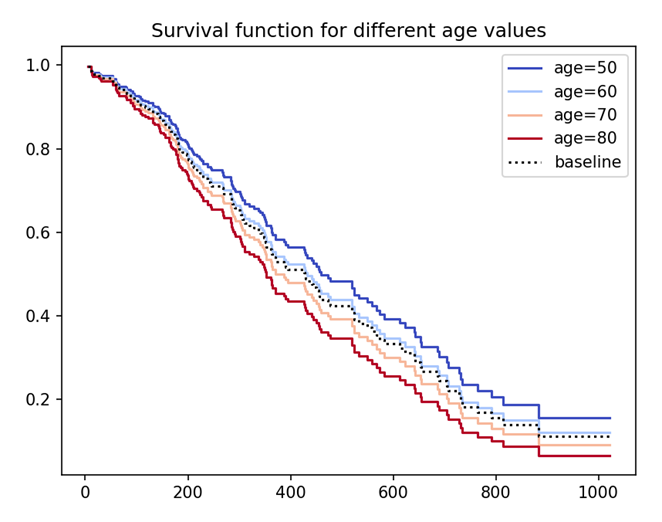
# Plot Partial Effects on Outcome
cph.plot_partial_effects_on_outcome(covariates = 'age', values = [50, 60, 70, 80], cmap = 'coolwarm')
plt.title("Survival function for different age values")
plt.show()
		    

I can also see who the survival changes as I change the covariate values.

I use the plot_partial_effects_on_outcome method to see how the survival changes for age group of 50,60,70 and 80 years old compared to their baseline.

It tells me that young patients have higher survival probabilities at any time.

#Check Proportional Hazard Assumption
print(cph.check_assumptions(df, p_value_threshold = 0.05))
		    

To verify the proportional hazard assumption, I use the check_assumptions() that return a log rank test statistics.

The null hypothesis assumes that the proportional hazard criteria met, while the alternative hypothesis infers that the proportional hazard assumption criteria violated.

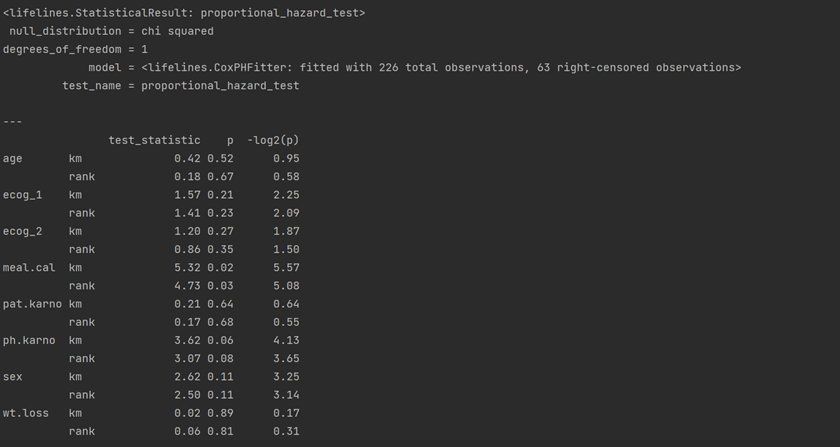
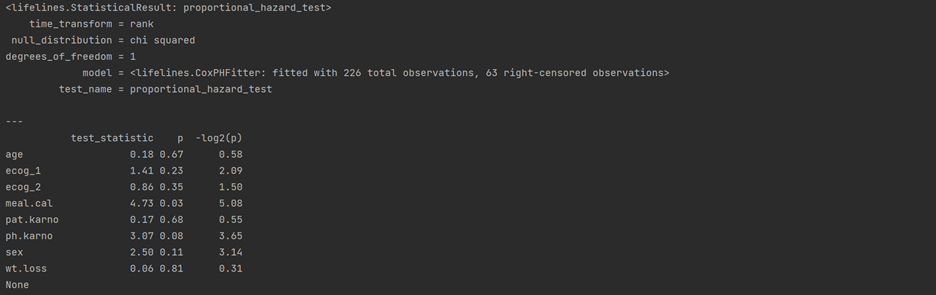
res = proportional_hazard_test(cph, df, time_transform='rank')
print(res.print_summary(decimals=3, model="untransformed variables"))
		    

I use another method to perform the same.

The result indicates that at 5% significance level, only mean.cal violoated the assumption. There are multiple approaches to deal with it. I can convert it to a binned category or use parametric Cox-PH model.

Accelerated Failure Time (AFT) Model

What is AFT?

Accelerated Failure Time (AFT) is one of the popular parametric models used in survival analysis. The model assumes that the survival function follows a parametric continuous distribution. For instance, one can assume a Weibull distribution or a Log-normal distribution.

The parametric AFT model assumes that survival function that derived from say two population (for example P and Q) are related by some acceleration factor lambda (λ), which can be modelled as a function of covariates.

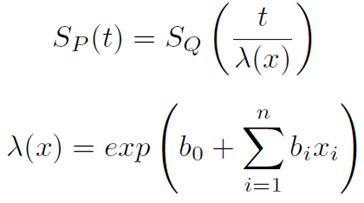
Acceleration Factor/Time Ratio as a function of covariates

Based on the covariates, the AFT model can accelerate or decelerate the failure times. The AFT model coefficients can be interpreted easily: a unit increase in a covariate means the average/median survival time changes by a factor of exp(b_i).

Identifying the best fitted distribution

There are many distributions available that we can fit. So the first step is to identify the best fit one. The common distributions include Weibull, Exponential, Log-Normal, Log-Logistic and Generalized Gamma.

# identify the best distribution
wb = WeibullFitter()
ex = ExponentialFitter()
log = LogNormalFitter()
loglogis = LogLogisticFitter()
# Fit to data
for model in [wb, ex, log, loglogis]:
    model.fit(durations = df["time"], event_observed = df["status"])
    print("The AIC value for", model.__class__.__name__, "is", model.AIC_)
		    

Initialize these common distribution objects.

Feed data into each one and see performance.

The scores indicate Weibull is the best.

# initialize model object
weibull= WeibullAFTFitter()
weibull.fit(df, duration_col='time', event_col='status')
weibull.print_summary()
		    

Initialize a Weibull model.

Feed data into the model.

Display summary.

A unit increase in covariate indicates that the mean/median survival time will change by a factor of exp(coefficient).

If the coefficient is positive, then the exp(coefficient) will be >1, which will decelerate the incident/event time. Similarly, a negative coefficient will reduce the mean/median survival time.

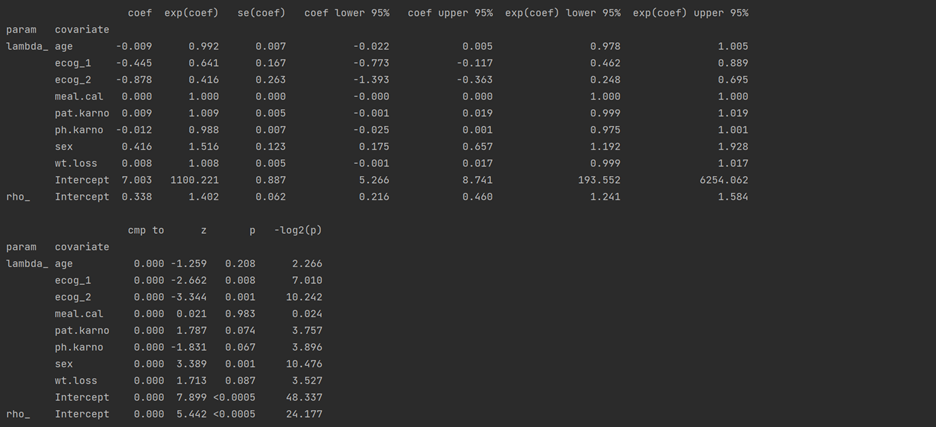
Example:

Sex containing [0: Male (base) and 1: Female] has a positive coefficient. It means being a female subject compared to male changes mean/median survival time by exp(0.416) = 1.516, approximately a 52% increase in mean/median survival time.

#Median Survival Time and Confidence Intervals
print("AFT median:"+ str(weibull.median_survival_time_))
print("AFT mean:"+str(weibull.mean_survival_time_))
		    

The estimated mean and median survival time.

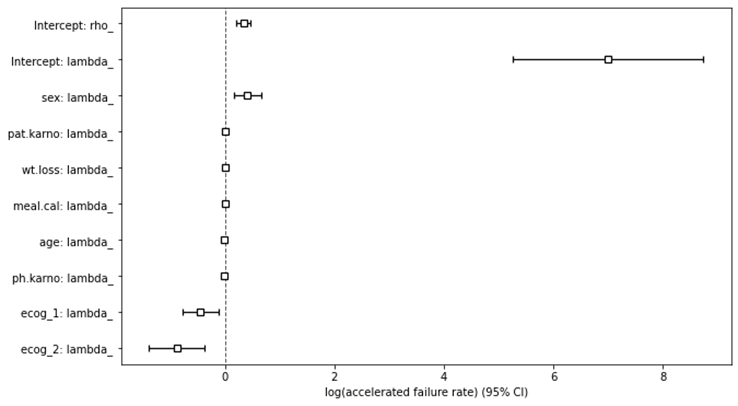
# plot variable ranking
plt.subplots(figsize=(10, 6))
weibull.plot()
plt.show()
		    

#Plot Partial Effects on Outcome (Weibull Regression)
plt.subplots(figsize=(10, 6))
weibull.plot_partial_effects_on_outcome('age', range(50, 80, 10), cmap='coolwarm')
plt.show()
		    

To see how survival changes as we change the covariate values, I use the method to see how the survival changes among 50.60.70.80 years old compared to their baseline function.

It clearly indicates young patients have higher survival probabilities than old patients.